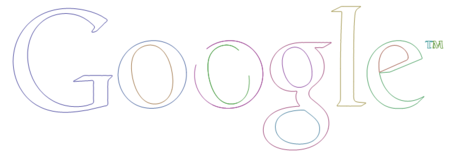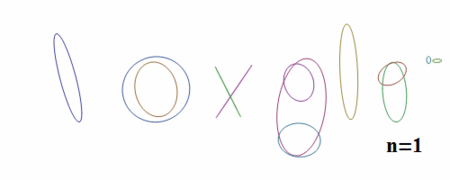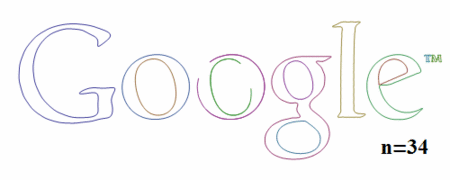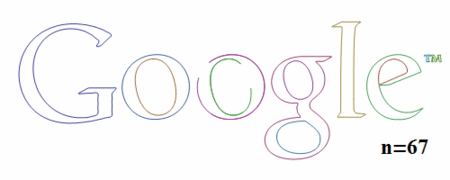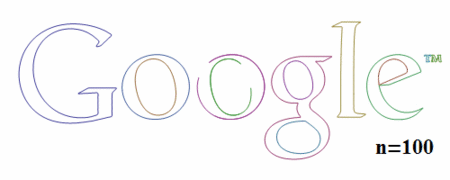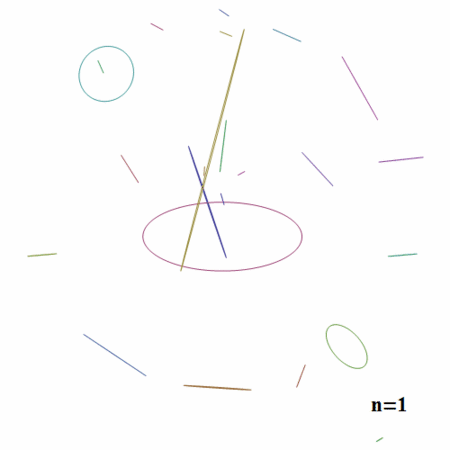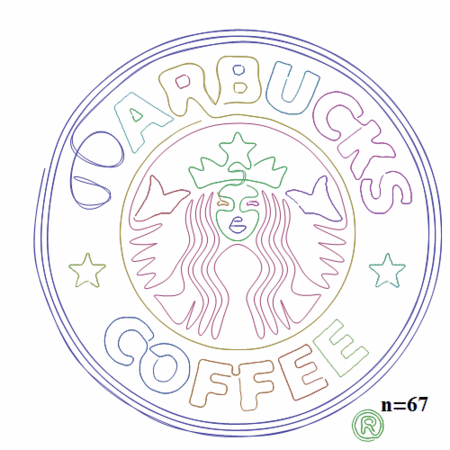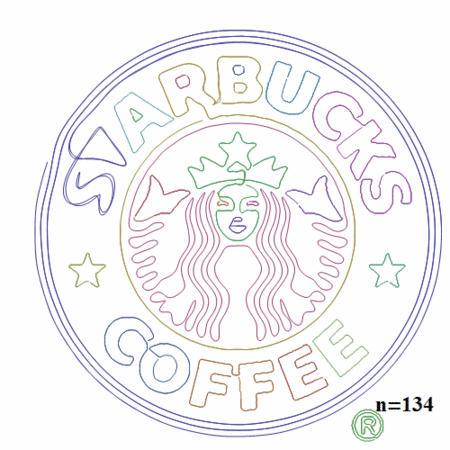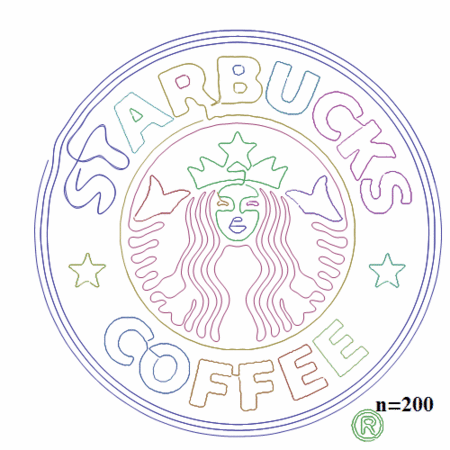Mathematicaで任意画像の輪郭を数式に変換する
330個の1000次方程式によるまどかマギカ pic.twitter.com/QnuOhXQfiT
— りんご (@aomoriringo) November 27, 2013
上記のような、任意の画像の輪郭を数式に変換するプログラムを紹介します。
発端
Wolfram|Alphaには「Person Curve」と呼ばれる類の検索結果が存在し、「Barack Obama Curve」「Hatsune Miku like curve」とか検索すると、その人物・キャラを表したパラメトリック方程式とそのプロット結果が表示されます。

これについては以下に示すようにたくさんの記事があり、存在自体は早くから知っていました。
数式が解明されてしまった初音ミク。その他キャラクターを色々試してみました | 猫と杓子
http://nlab.itmedia.co.jp/nl/articles/1305/02/news063.html/
さまざまな顔を描画できる数式|WIRED.jp
そして数日前にMathematicaで作り方を解説している記事(Making Formulas… for Everything—From Pi to the Pink Panther to Sir Isaac Newton—Wolfram Blog)を教えてもらったので、それを参考にしてやってみました。(というかほぼコピペ)
方針
以下のステップからなります。
実践
以下を実行させるための全てのMathematicaコードは以下のgistを参照してください。
任意画像の輪郭を数式に変換してプロットする (Mathematica ver.8)
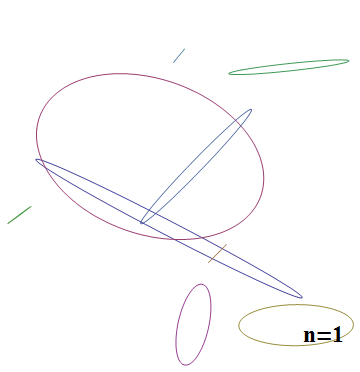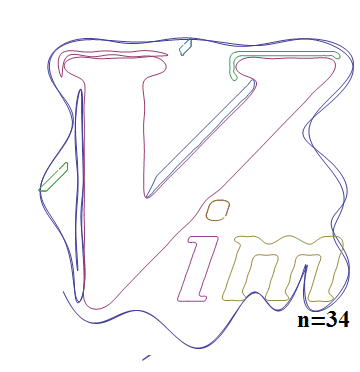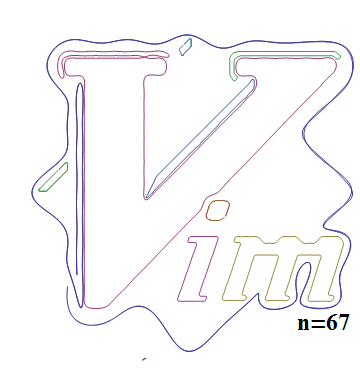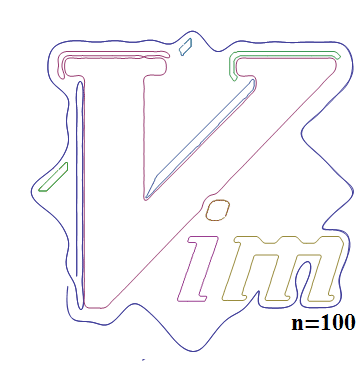
以下に示すvimのロゴ画像を使用して、数式に変換される過程を見てみましょう。
ちなみに私は普段emacsを使っています。

エッジ抽出
画像を引数にとり、エッジの抽出結果をバイナリ画像として返すEdgeDetect関数を使用します。
img = Import[imageURL]; edgeImage = Thinning[EdgeDetect[ColorConvert[ ImagePad[Image[Map[Most, ImageData[img], {2}]], 20, White], "Grayscale"]]]

このEdgeDetectの精度が素晴らしく、最終的なプロット結果が良い一因となっています。
ベタ塗りの部分が多い画像、つまりロゴやアニメの絵などは良い結果になりやすく、グラデーションが多かったり、現実の写真の場合は想定しない結果になってしまうことが多いです。
エッジを複数の点群に分割
方針で示したような処理を行い、複数の点群に分割します。
edgePoints = {#2, -#1} & @@@ Position[ImageData[edgeImage], 1, {2}];
SeedRandom[2];
hLines = pointListToLines[edgePoints, 16];
Graphics[{ColorData["DarkRainbow"][RandomReal[]], Line[#]} & /@
hLines]
以下は各点群ごとに別々の色をつけ、線でつないで描画した図です。この時点ではまだ数式になっていません。

数式に変換
各点群ごとにフーリエ変換を行い、数式に変換します。
(フーリエ変換についてはフーリエ変換の本質などを参考にしてください。)
fCs = fourierComponents[hLines]; Show[ParametricPlot[ Evaluate[makeFourierSeries[#, t, 100] & /@ fCs], {t, -Pi, Pi}, Axes -> False]]
ここで引数に与えている「100」がフーリエ変換後の数式の次数となります。大きいほど精度がよくなります。

次数が上がっていくと、どのようにプロットが変化していくかを見てみましょう。
Partition[Table[paraplot[n], {n, 1, 12}], 4] // GraphicsGrid
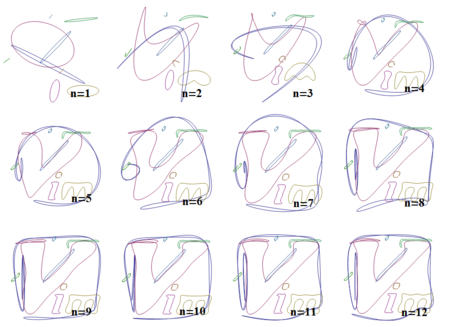
n=1の場合楕円のみが描画されていますが、nが大きくなるにつれてだんだんと元の画像の形に近づいていることがわかります。
これらの過程をgifにしてみたところ、とても面白い。
外側の線が一番長く、収束に一番時間がかかっています。
このことから、一番長い線分がどれだけ速く収束するかによって、何次まで近似すれば十分な精度が得られるかどうかが決まってくることが推測できます。
最後に、上記Vimのロゴの数式を表示してみます。
curves = makeFourierSeries[#, t, 200] & /@ fCs; Style[Map[Short, Rationalize[curves, 0.002]], 16] // TraditionalForm

この例の場合、エッジ抽出の結果は9個の点群に分解され、9個の数式になりました。
1つの数式は200次近似を行ったためそれぞれ201の項を持ちます。(全部表示すると長すぎるので、上記結果は途中を省略して表示しています)
いろいろやってみる
Coca-Cola


意外にも「oca」の部分が長い線分となっており、割と時間がかかっています。
Unilever

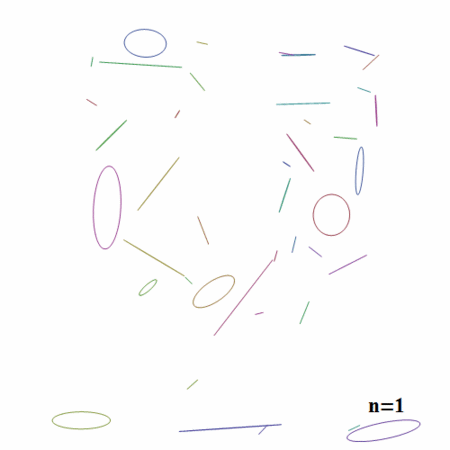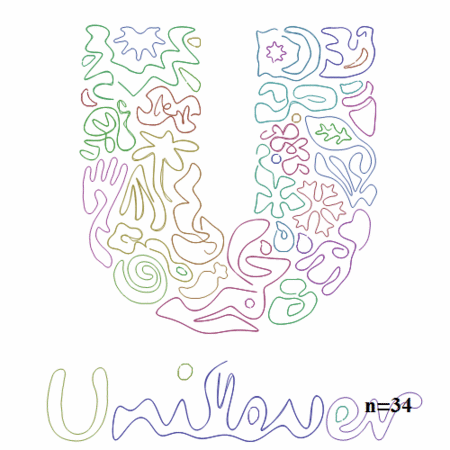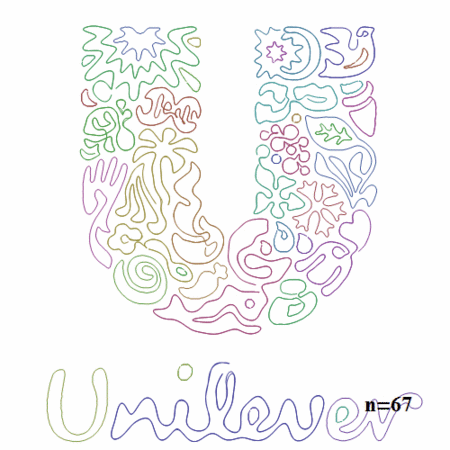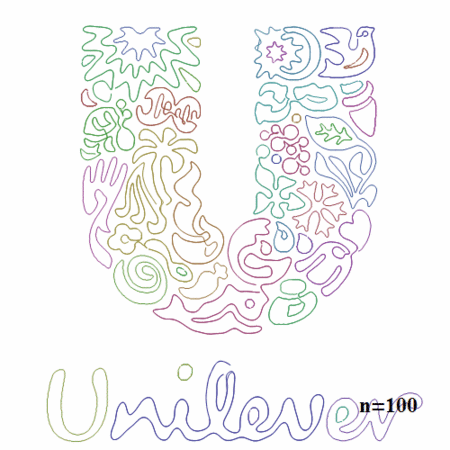
ロゴがかなり複雑でしかもエッジ抽出はしやすそうということでやりました。
個々の線分は短いので収束は速いですね。それにしても、カラフルでとてもきれい。
実行について
この記事で紹介しているプログラムはMathematicaで書かれたものです。Mathematicaは商用なので、この状態だと持っている人しか実行できません。
編集できないという形に限定すると、無料で提供されているWolfram Mathematica PlayerとかWolfram CDF Playerを使うことで実行させることができます。
ただ、URLや次数などを変更できる形にできるかどうかわからないので、もし配布して欲しいという声があればやってみようと思います。
2014/03/11 追記
@YVT さんが画像輪郭をフーリエ近似してその画像プロットを返すサービスを作成されていました。これで皆さん自由にフーリエ近似できます、すごい!
Contour
619個の1000次方程式でアイドルマスター pic.twitter.com/DQBLZx9tvN
— りんご (@aomoriringo) November 29, 2013
以上です。Mathematica環境に触れる方はぜひお試しください。
2013/12/04 追記
今Mathematicaが無料で使用できると話題のRaspberryPiですが、RaspberryPi上でも上記コードが動くことを確認して下さった方がいました。